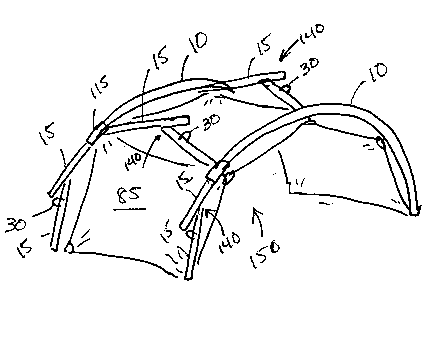
A segmented, articulated pole member structure is constructed of pivotally interconnected, pole segments. The pole segments are arranged 1 offsetting fashion such that in their disassembled state they may be folded into a compact bundle for storage. In the assembled state, adjacent pole segments are retained under tension in fixed angular position relative to each other by a pivoting connection and an engagement loop or similar structure. Applications for the pole member structure include the construction of flexible structures such as tents and shelters, and support frames for mounting, supporting, or suspending articles in a desired shape.
BACKGROUND OF THE INVENTION
Field of the Invention
The invention relates generally to structural members of the type typically used in flexible structures, such as tents, shelters and the like, and more particularly to resilient pole members. The invention further relates to articulated structural members which may find use as a frame in support applications, such as for mounting, supporting or suspending articles in a desired shape.
Description of Related Art
In the area of flexible structures, including tents, shelters, and the like, it has long been common practice to employ one or more resilient pole members. Typically, the pole members are held under tension in a desired shape to define the structure and to support a membrane defining a sheltered space. Examples include dome type tents, vault type shelters, and the like. The inventor named herein has in the past invented numerous flexible structures employing a variety of resilient pole members and arrangements.
Typically, the resilient pole members employed are constructed of aluminum, graphite, or similar resilient materials. Both one piece and segmented pole members are known. One piece pole members have the advantage of strength and ease of assembly. However, segmented pole members have the advantage that they can be disassembled and compactly stored, which may be important in certain applications, such as lightweight backpacking tents.
Typically segmented pole members have the segments connected end to end, for example using a male-female connection and a friction fit. Hub connections are also known and are shown in one or more of the above-identified Patents. In order to prevent the loss of individual segments, which would render a pole member useless, and to assist in the pole assembly process, it has been known to connect the individual segments together in a more or less permanent fashion, for example using a “shock-cord.” A “shock-cord” is typically used with pole members that are hollow and is typically a thin elastic band or cord that fits through the hollow centers of the pole member segments and is knotted at each end. While a shock-cord advantageously tends to avoid the loss of pole segments, it does not necessarily add any strength to the pole member structure itself.
Generally, resilient pole members of the type commonly used in constructing flexible structures such as tents are not very flexible in the applications to which they can be put. In order to be easily tensioned, they are typically made of light weight, resilient, and non-rigid materials. If such pole members are to be used with larger structures, heavier and more rigid materials must be used to withstand the increased loading of the elements, as well as the increased weight of the membrane or membranes defining the sheltered space. Heavier and more rigid pole members are significantly more difficult to tension, i.e., bend. Significant effort, perhaps aided by tools such as tensioners, is typically required to tension such pole members during assembly of the structure. Moreover, there can be danger involved in the disassembly of flexible structures employing such heavier, more rigid pole members due to the significant tensioning forces that are released when the structure is disassembled.
For the same reasons, such pole members are typically not useful in other support applications, such as providing a frame for mounting or suspending articles in a desired shape. For example, such pole members are typically not suitable for use as a trellis for creeping vines, or as a frame for supporting flowers or balloons in a selected shape.
The present invention provides a segmented, articulated pole member structure that is light in weight, compact to store, strong, easily assembled and disassembled, and flexible in application. It will find application in constructing both small and large flexible structures, as well as a support frame for mounting, suspending or supporting articles in a desired shape.
SUMMARY OF THE INVENTION
The features and advantages of the present invention reside in a pole member structure having a plurality of segments. Each segment has a pivoting connection with each adjacent segment. Each segment also has a connector for selectively connecting the pole segment with one of its adjacent pole segments so that adjacent pole segments are retained in a fixed angular position relative to their pivoting connection when the pole member structure is tensioned.
The individual pole segments may be rigid or resilient, and the connector may be a ring, loop, or other suitable connector. The ends of the adjacent segments may overlap and the longitudinal axes of the adjacent segments maybe offset to facilitate folding the pole member structure into a compact bundle for storage.
In another aspect of the invention, the pole member structure is provided with base supports to engage its opposite ends and support it in an upright position at a selected angle. Such base supports may include fabric pockets or the like in a flexible structure, or more rigid supports such as rigid tubes or stakes to support the pole member structure on the ground or a floor or other base. In this aspect of the invention, the pole member structure can be used as a frame for mounting, supporting or suspending articles in a desired shape.
In yet another aspect of the invention, a plurality of articulated, segmented pole member structures are tensioned and arranged in a desired shape to define a flexible structure such as a dome or vault. A membrane is connected to at least some of the pole member structures to define a sheltered space.